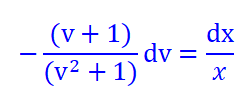สมการเอกพันธ์เชิงเส้น
Homogeneous Linear Equation
dy/dx=(y-x)/(y+x)
วิธีทำ
อยู่ในรูป
เป็นสมการที่1
ให้เช็คก่อนว่าเป็นสมการเอกพันธ์เชิงเส้นหรือไม่
โดยที่
f(x,y)=f(kx,ky)
มีตัวแปรตรงไหน
ให้ใส่kที่นั้น
ดึงkออกจากสมการ
kตัดกัน
เป็นสมการเอกพันธ์
ดิฟy โดยใช้สูตรผลคูณ (หน้าดิฟหลังบวกหลังดิฟหน้า)
นำสมการที่ได้ไปแทนในสมการที่1
จัดรูปใหม่
xตัดกัน
ย้ายข้างvไปลบ
ทำเศษส่วนร่วม
จะได้
vลบกัน ดึงลบออก
ขั้นตอนนี้ทำเหมือนสมการแยกตัวแปรได้
โดยย้ายข้างจัดรูปให้dxอยู่กับx ให้dv อยู่กับv สมการที่2
แยกเศษส่วน
ใส่อินทิเกรตทั้ง2ข้าง
กระจ่ายอินทิเกรต
ใช้สูตรอินทิเกรต
จะได้
แทนค่าจะได้
อินทิเกรตได้
คืนค่า U
นำ2คูณเข้าทั้งสมการ
คืนค่าV
จัดรูปใหม่
จากโดย
กฎของลอการิทึม
ใช้กฏของลอการิทึม
นำลบคูณเข้าวงเล็บ
และย้ายln x^2 มาลบ
ln x^2 มาลบกัน
หรือ เอาลบคูณทั้งสมการ
ตอบ
วีดีโอ
วีดีโอไม่ได้อธิบาย