จงหาคำตอบของสมการเอกพันธ์เชิงเส้น
จัดรูปให้อยู่ใน
จัดรูปสมการเป็นสมการที่1
ให้เช็คก่อนว่าเป็นสมการเอกพันธ์เชิงเส้นหรือไหม
โดยที่
f(x,y)=f(kx,ky)
มีตัวแปรตรงให้ใส่kที่นั้น
ดึงkออกจากสมการ
kตัดกัน
เป็นสมการเอกพันธ์
กำหนดตัวแปร
ดิฟ X โดยใช้สูตรผลคูณ (หน้าดิฟหลังบวกหลังดิฟหน้า)
นำสมการที่ได้ไปแทนในสมการที่1
yตัดกัน
ย้ายข้างvไปลบ
จัดรูป
ขั้นตอนนี้ทำเหมือนสมการแยกตัวแปรได้
โดยย้ายข้างจัดรูปให้dyอยู่กับy ให้dv อยู่กับv สมการที่2
อินติเกรตทั้ง2ข้าง
สูตรที่ใช้
อินติเกรตเสร็จ
คืนค่าv
จัดรูป
จากโดย
กฎของลอการิทึม
แยกln yออก
ย้ายln yออก
จากโดย
กฎของลอการิทึม
เอาln yมารวมกัน
นำ เอกซ์โพเนนเชียล (e) เทคทั้งสมการ
จากโดย
กฎของลอการิทึม
จะได้
ตอบ
วีดีโอ
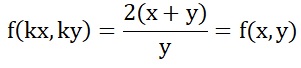
ไม่มีความคิดเห็น:
แสดงความคิดเห็น